
이상 기체 방정식은 기체의 상태를 설명하는 방정식입니다. 하지만 실제 기체에 적용하기에는 무리가 있는데요. 이는 이상 기체는 가상의 기체이기 때문입니다. 이상 기체와 이상 기체가 되기 위한 조건, 실제 기체를 나타낼 수 있는 방정식에 대해 알아보도록 하겠습니다.
이상 기체 방정식
이상 기체 방정식은 기체의 상태를 서술하는 방정식으로 '보일의 법칙', '샤를의 법칙', 아보가드로 법칙을 모두 아우릅니다.
보일의 법칙: 기체의 부피는 압력에 반비례한다. V∝1/P
샤를의 법칙: 기체의 부피는 절대온도에 비례한다. V∝T
아보가드로 법칙: 기체의 부피는 기체의 양(mol)에 비례한다. V∝n
위 세 법칙을 종합하고 비례 상수를 넣어주면 아래의 방정식이 됩니다. 특히 비례 상수는 R로 표현하며 기체 상수(gas constant)라고 합니다.
PV=nRT
*P = 압력, V = 부피, n = 양(mol), T = 절대온도
다만, 이 방정식은 이상 기체에서만 성립하며, 실제 기체를 설명하기 위해서는 보정된 방정식이 필요합니다.
이상 기체가 되기 위한 조건
이상 기체 방정식은 기체의 상태를 나타내고는 있지만 그것이 성립하는 이유는 설명하지 않습니다.
기체 분자 운동론(kinetic molecular theory)은 기체 분자의 운동으로 기체의 성질을 설명하고 있는데요 이 이론에 따르면 다음을 만족시키는 이상 기체를 가정합니다.
1. 기체 분자는 끊임없이 불규칙한 직선 운동을 한다.
2. 기체 분자는 완전 탄성 충돌을 한다.(충돌 후 에너지의 손실이 없다.)
3. 기체 분자의 크기는 분자들이 차지하는 공간에 비해 매우 작으므로 무시한다.(분자 자체의 부피는 0)
4. 기체 분자 사이에 힘이 작용하지 않는다.(인력이나 반발력이 작용하지 않는다.)
5. 기체의 평균 운동에너지는 절대 온도에 비례한다.(분자의 종류와 무관)
압축 인자와 실제 기체
이상 기체 방정식은 이상 기체의 상태를 설명하는데요. 이상 기체는 실제로 존재하지 않는 가상의 기체이므로 실제 기체에 이상 기체 방정식을 적용하면 완벽하게 들어맞지 않습니다.
그렇다면 '실제 기체가 이상 기체에서 얼마나 벗어나 있을까?'는 압축 인자를 이용하여 비교할 수 있습니다.
압축 인자
기체의 PV/nRT 값을 측정해 봅시다. 이상 기체 방정식에 따르면 PV=nRT 이므로 PV/nRT=1이 됩니다.
하지만 실제 기체에서 PV/nRT 값은 1에서 벗어나는데요.
여기서 분자의 PV는 실제 기체의 압력과 부피이고
분모의 nRT는 이상 기체라면 PV이고 이는 이상 기체의 압력과 부피입니다.
두 압력은 동일하니 PV/nRT는 이상 기체의 부피에 대한 실제 기체의 부피 비를 의미하며 이를 압축 인자라고 합니다.

즉 압축 인자가 1에 가까울수록 이상 기체에 가깝다고 볼 수 있는 것이지요.
이상 기체와 실제 기체와의 차이

위 그래프를 보면 실제 기체의 압축 인자는 1이 아님을 알 수 있습니다.
압축 인자가 1보다 크면 실제 기체의 부피가 이상 기체의 부피보다 큰 것을
압축 인자가 1보다 작으면 실제 기체의 부피가 이상 기체의 부피보다 작은 것을 의미합니다.
실제 기체가 이상 기체와 차이를 보이는 이유는 실제 기체는 분자 자체의 크기가 존재하고 분자 간의 인력 또는 반발력이 작용하기 때문인데요.
Z<1 : 분자 간의 인력의 영향
Z>1 : 분자 자체 크기의 영향
반 데르 발스 방정식
실제 기체는 이상 기체 방정식에 적용할 수 없기에 이를 보정하기 위한 새로운 식이 필요했습니다.
네덜란드 물리학자 반 데르 발스(Johannes Diderik van der Waals)는 1873년 실제 기체에 적용할 수 있는 식을 제안했고 1910년에 노벨 물리학상을 수상하게 됩니다.
반 데르 발스 방정식(van der Waals' gas equation)은 기존의 이상 기체 방정식에서 실제 기체의 특성을 고려하여 일부 보정해 준 형태의 방정식입니다.

반 데르 발스 방정식의 a, b 인자는 실제 기체를 보정하기 위함입니다.
실제 기체는 분자 간의 인력이 작용하여 이상 기체에 비해 압력이 낮게 나타납니다. a 인자는 이를 보정해 주지요.
또한 실제 기체는 분자 자체의 크기 때문에 이상 기체에 비해 부피가 크게 측정됩니다. 따라서 b 인자는 기체 자체의 크기를 제외해 주는 셈이지요.
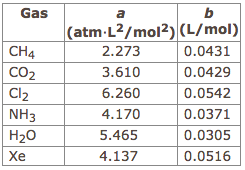
이 두 인자는 기체의 종류에 따라 달라지며
극성이거나 분자량이 커서 인력이 강한 분자일수록 a 값이 클 것이고,
분자량이 커서 분자 자체의 크기가 큰 분자일수록 b 값이 커지겠지요.
'공부합시다 > 화학 이야기' 카테고리의 다른 글
| 2024학년도 9월 모의고사 화학1 19번[중화 반응의 양적 관계] (0) | 2023.09.07 |
|---|---|
| 과학 동아리 기체의 분자량 측정 실험, 이상기체 방정식의 활용 (0) | 2023.08.29 |
| 오차의 원인 및 유효숫자 처리 방법 (0) | 2023.08.18 |
| 이성질체(isomer)의 종류와 분류 (0) | 2023.08.12 |
| 시성식과 작용기, 구조 이성질체 (0) | 2023.08.12 |



